这篇文章上次修改于 330 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

数据结构——二叉树先序、中序、后序三种遍历

一、图示展示：

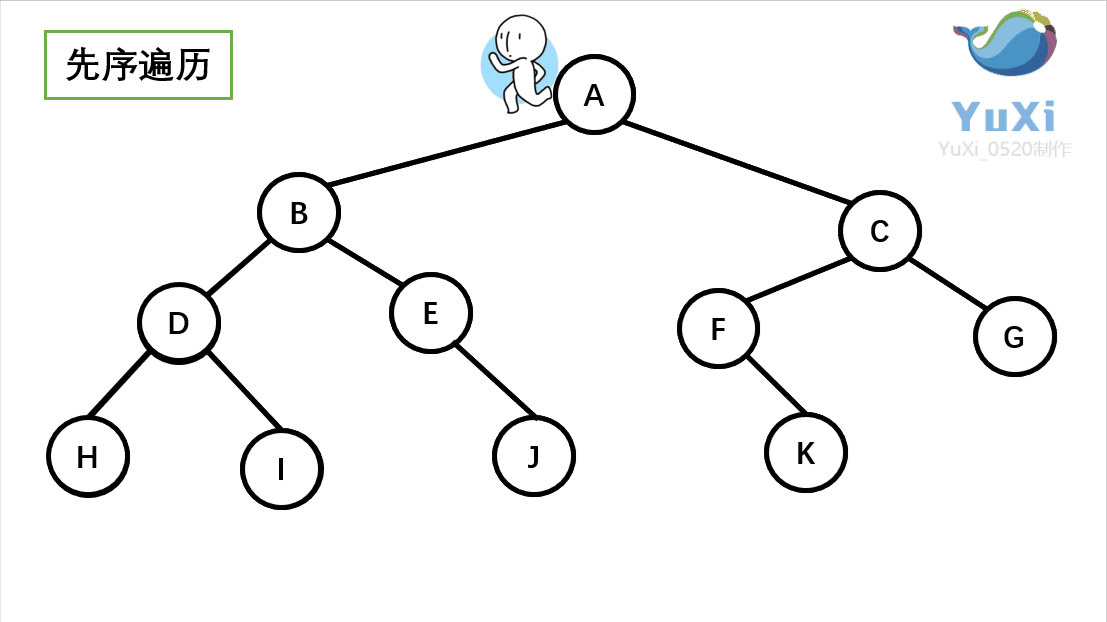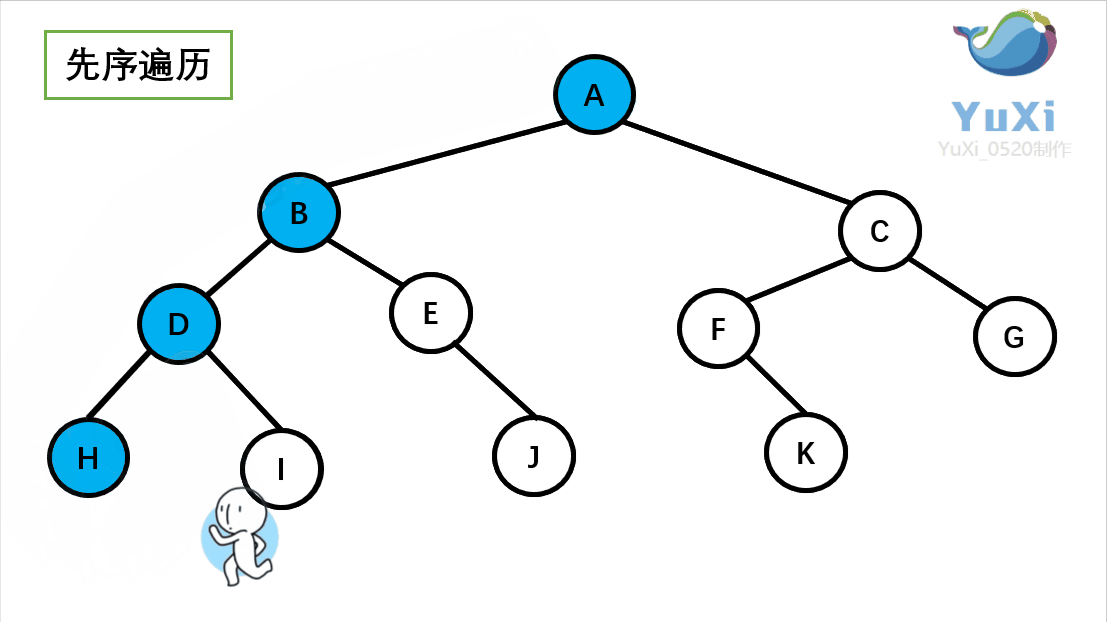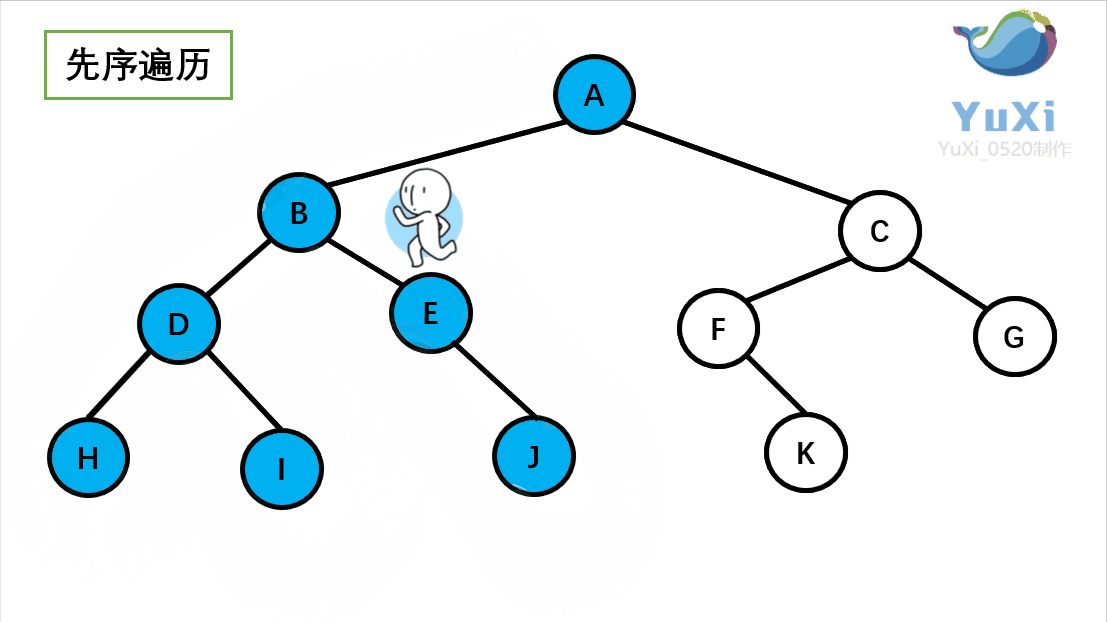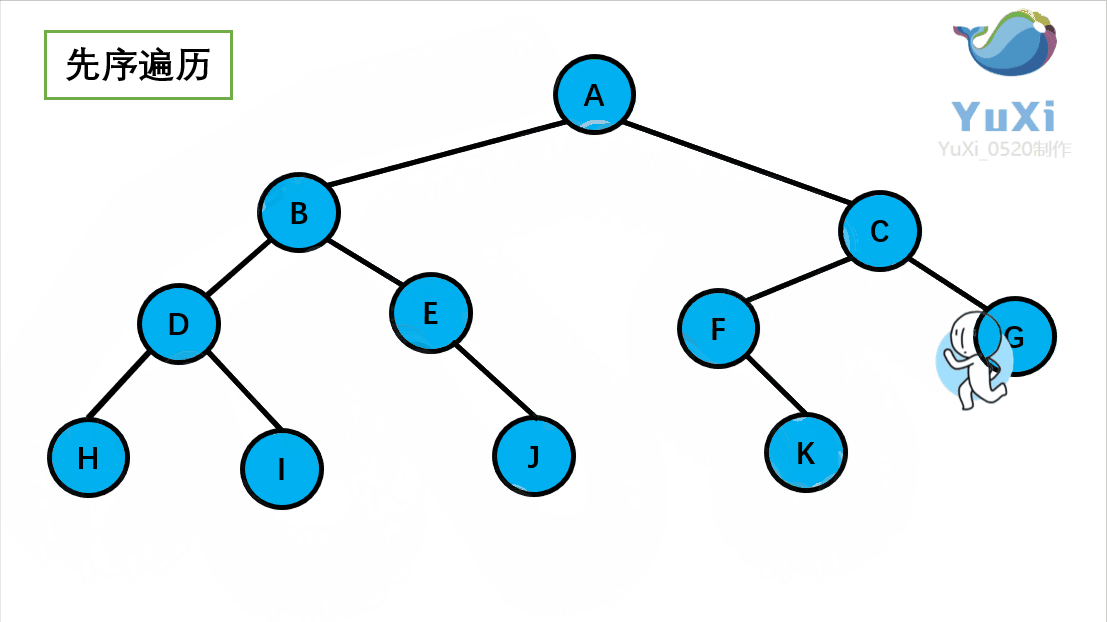
（1）先序遍历

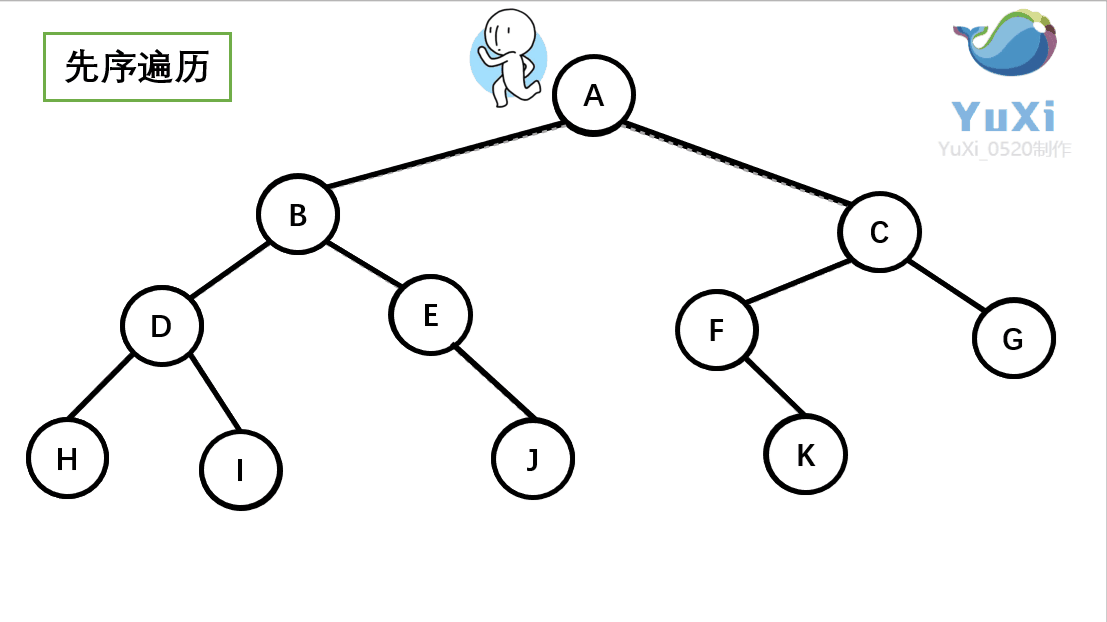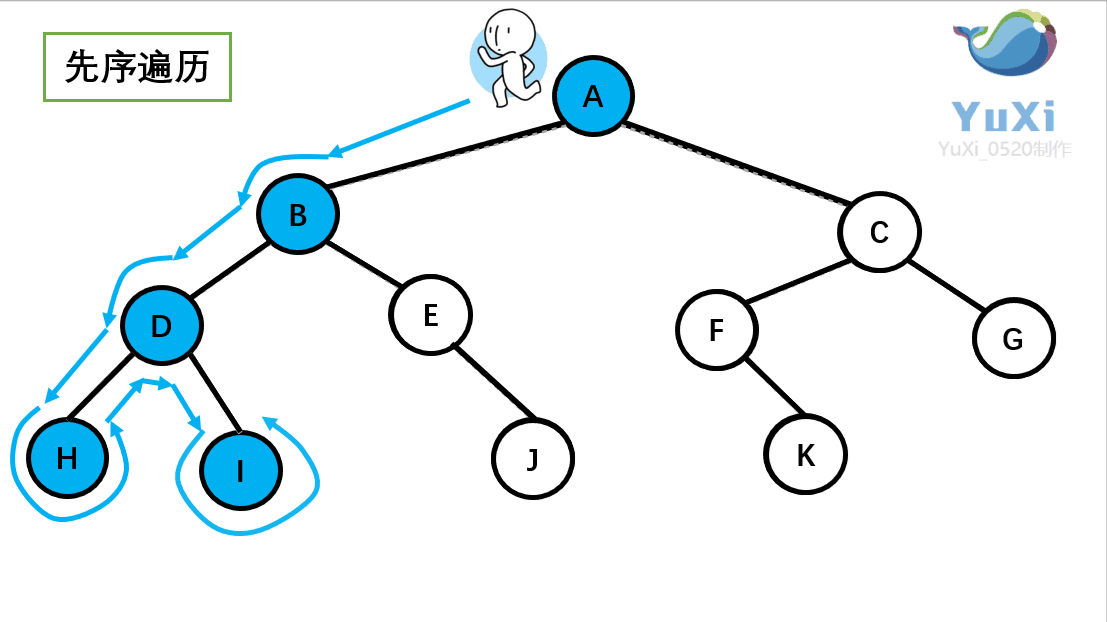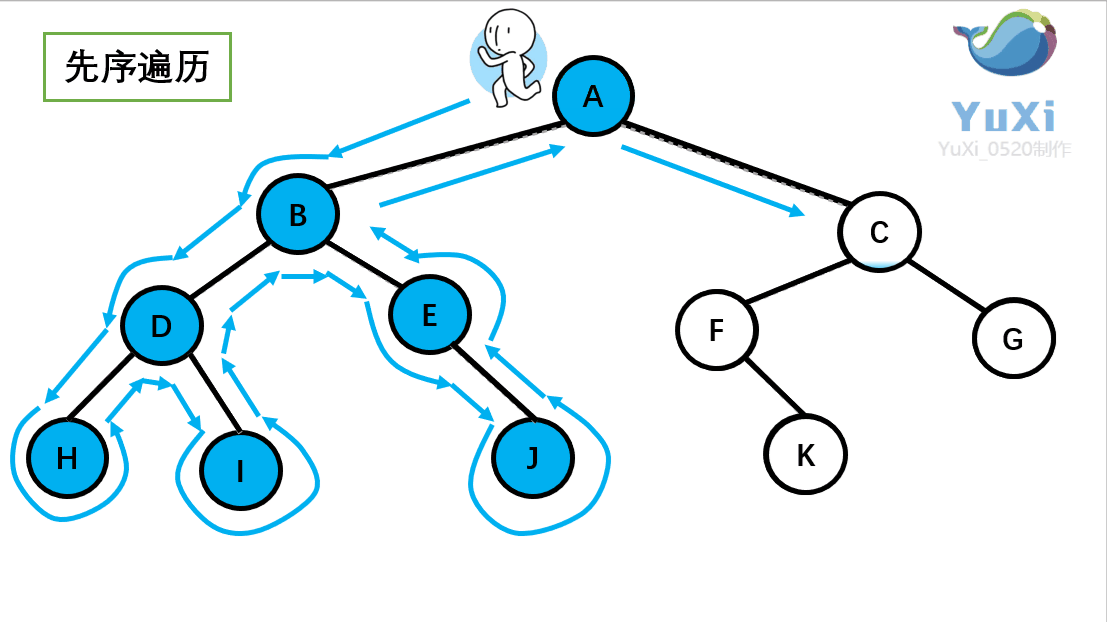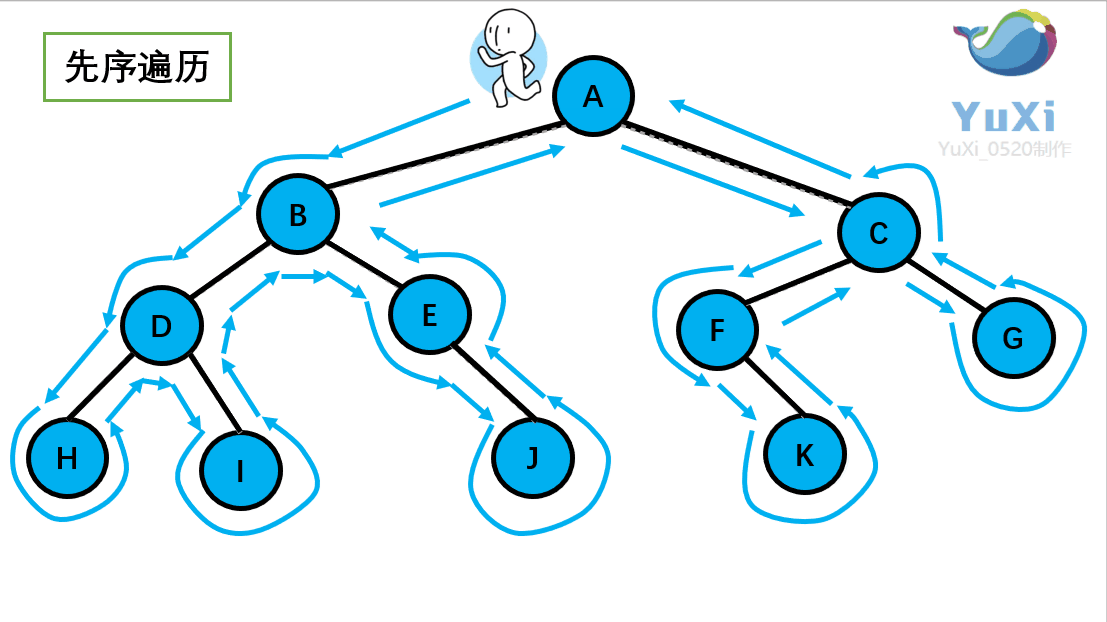
先序遍历可以想象为，一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果

先序遍历结果为：A B D H I E J C F K G

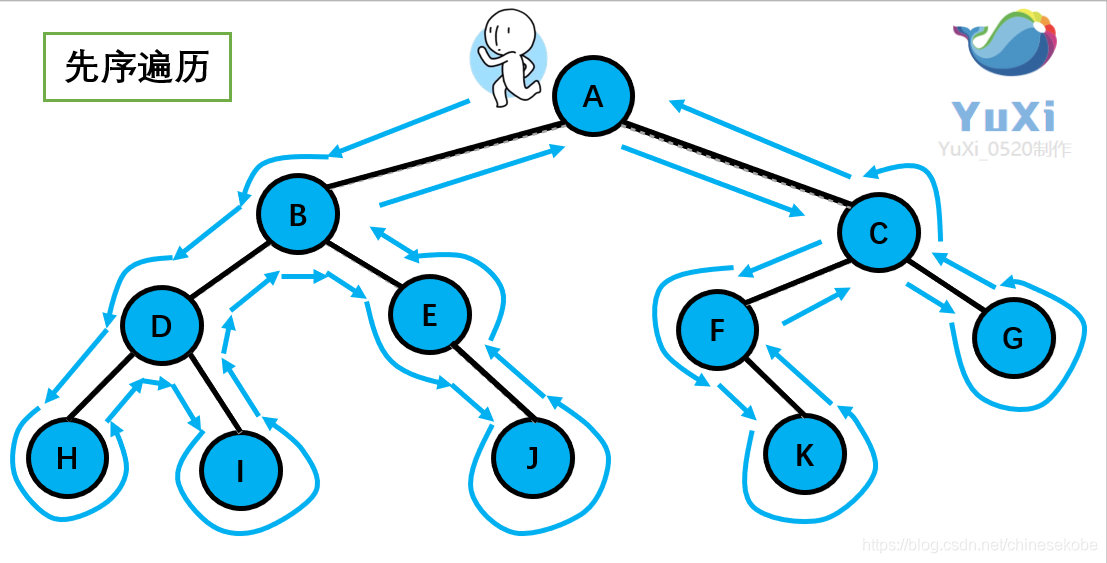
在这里插入图片描述
动画演示：

记住小人沿着外围跑一圈（直到跑回根节点），多看几次动图便能理解

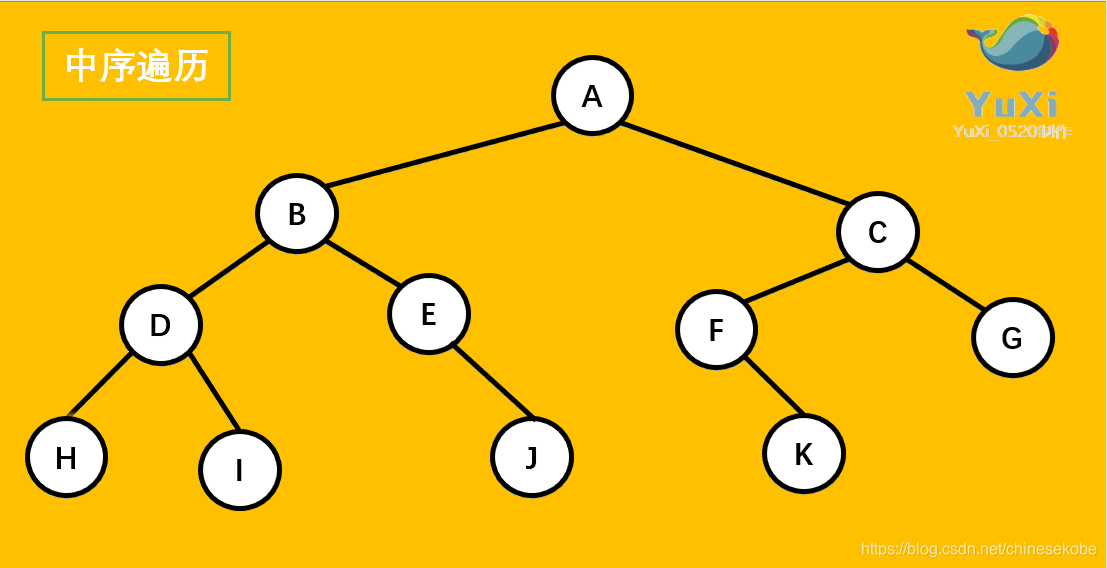
在这里插入图片描述
在这里插入图片描述

（2）中序遍历

中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数，得出的结果便是中序遍历的结果

中遍历结果为：H D I B E J A F K C G

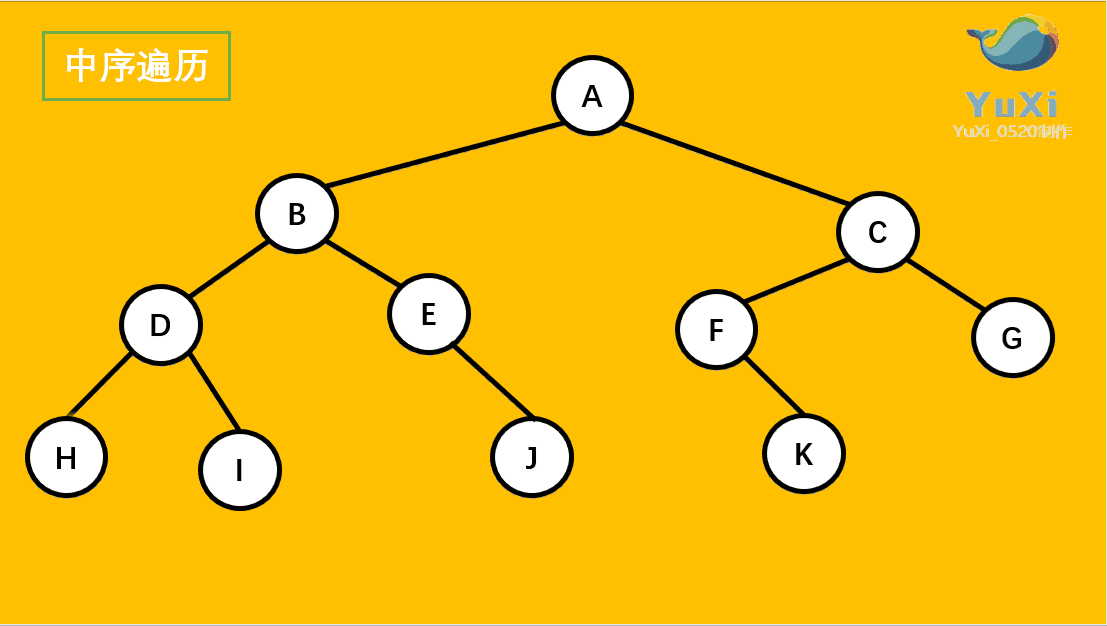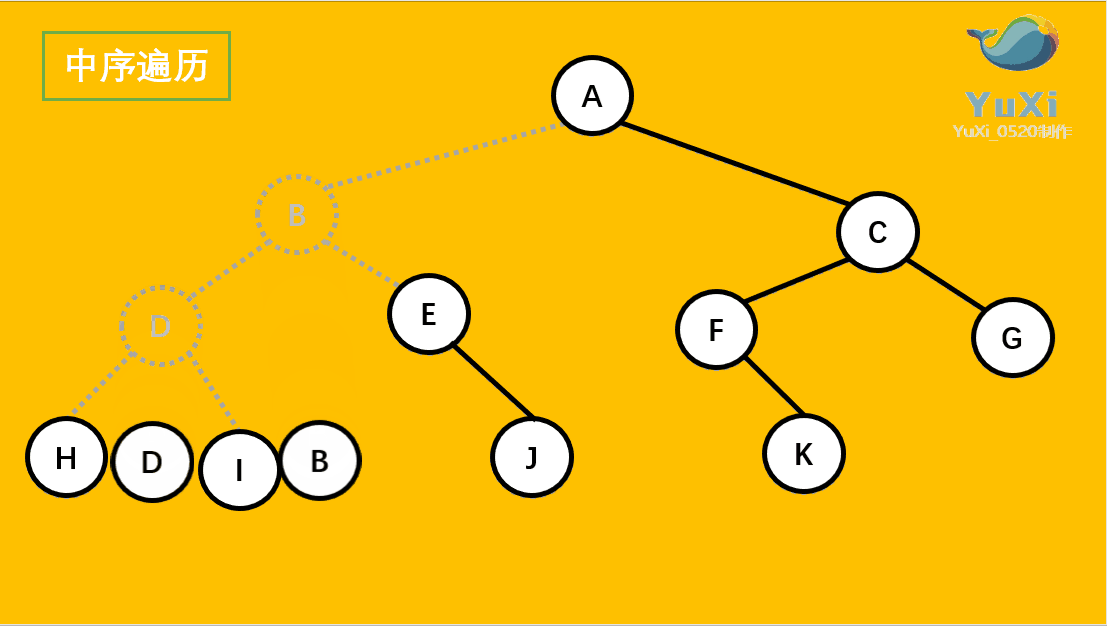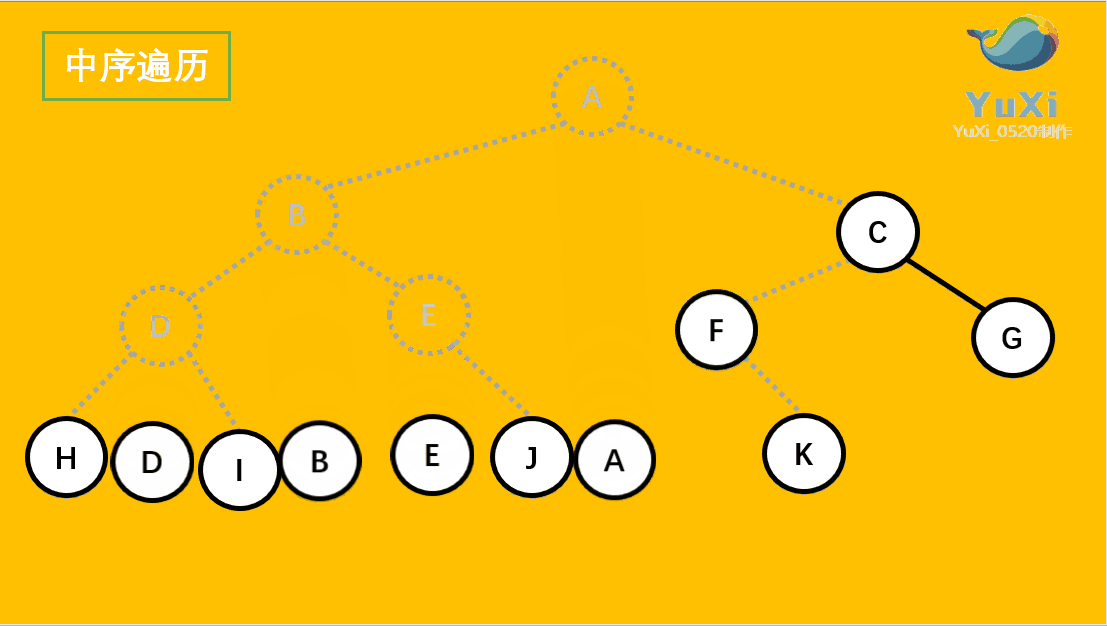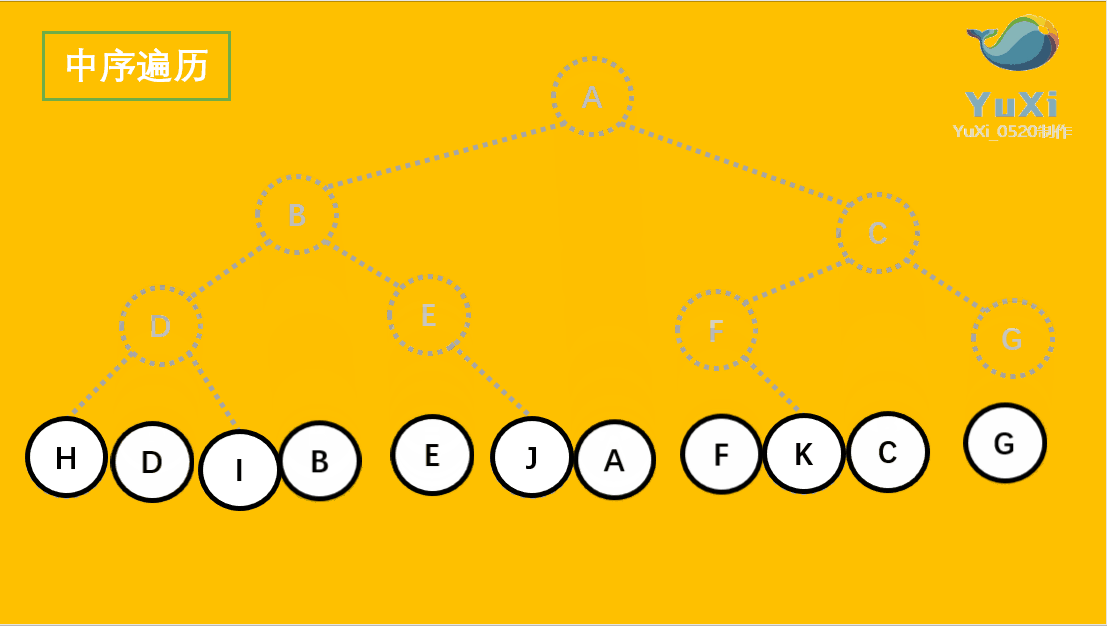
在这里插入图片描述

动画展示：

记住，中序遍历就是从最左边开始，把每个节点垂直投影到同一直线上，然后从左往右读值就可以了，多看几遍动图就理解了

在这里插入图片描述

（3）后序遍历

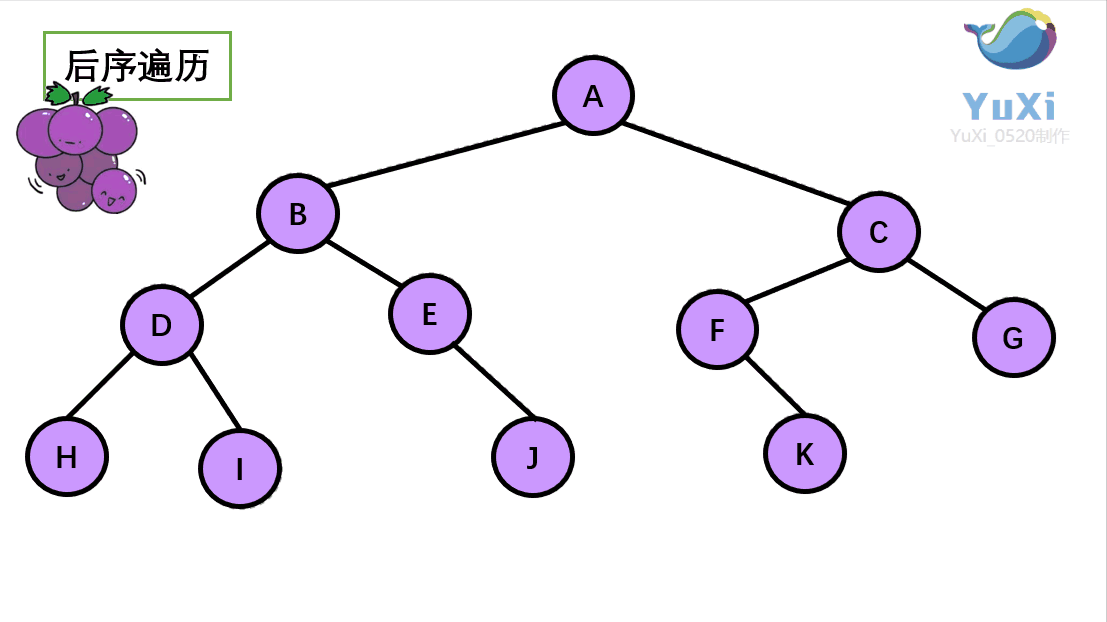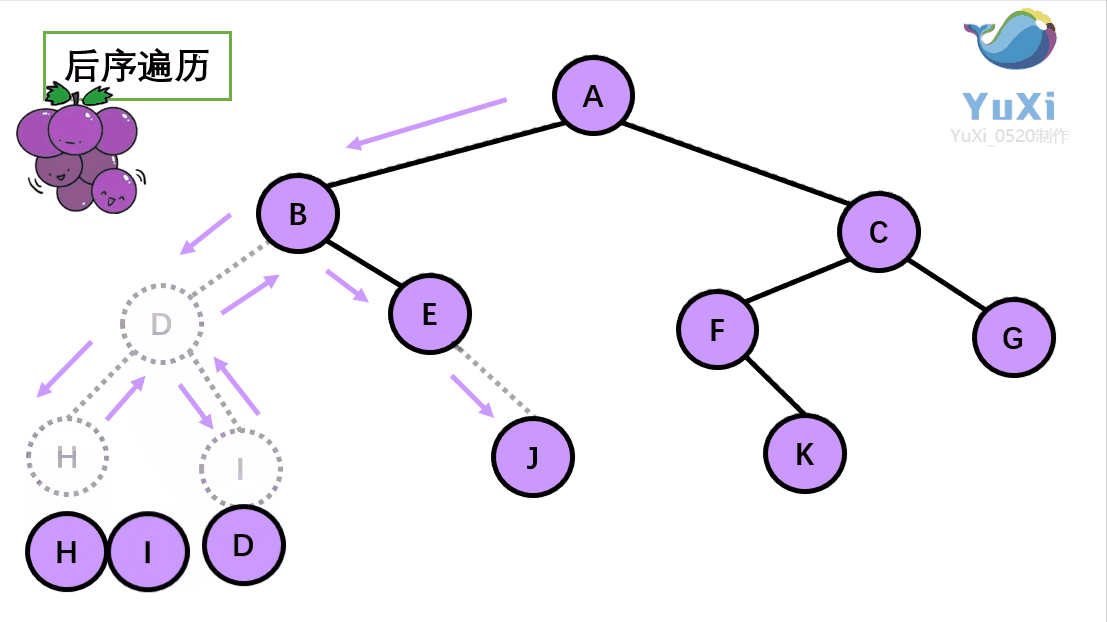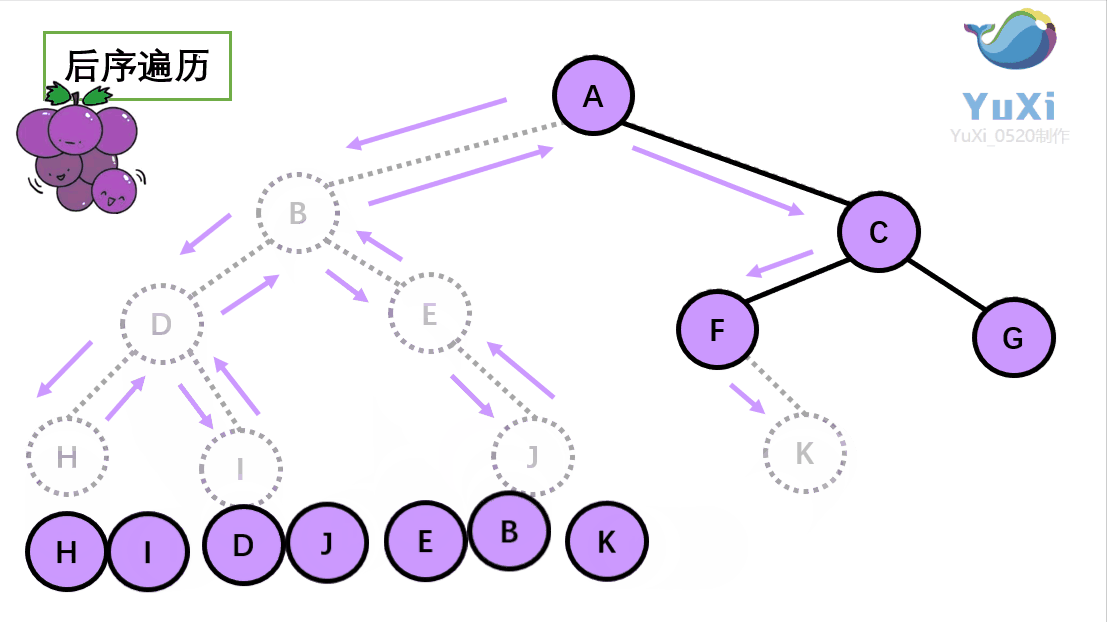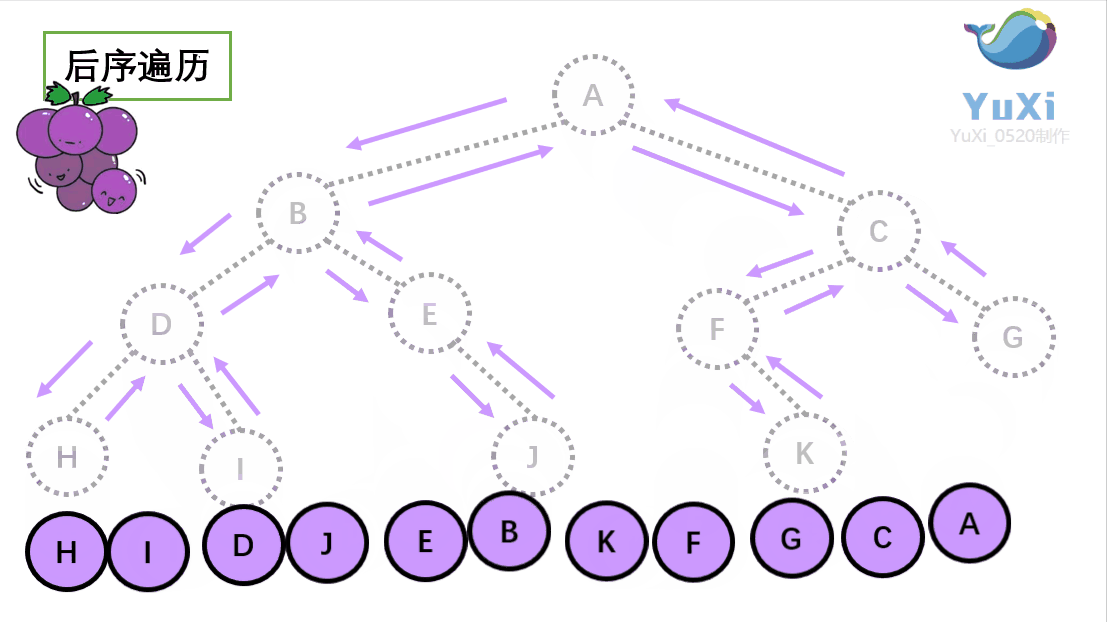
后序遍历就像是剪葡萄，我们要把一串葡萄剪成一颗一颗的。

还记得我上面提到先序遍历绕圈的路线么？（不记得翻上面理解）

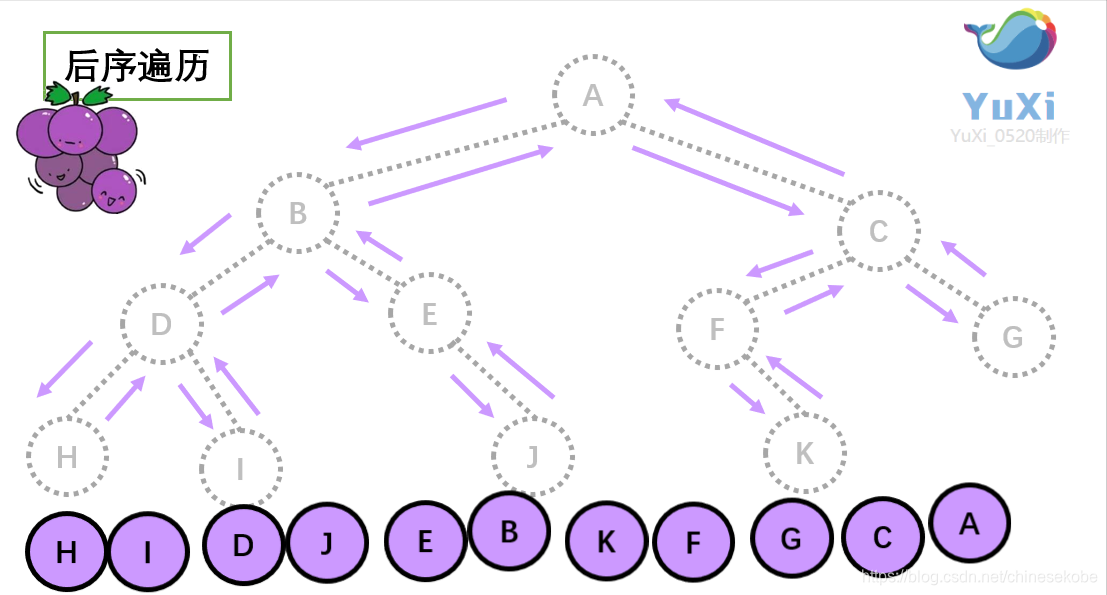
就是围着树的外围绕一圈，如果发现一剪刀就能剪下的葡萄（必须是一颗葡萄）（也就是葡萄要一个一个掉下来，不能一口气掉超过 1 个这样），就把它剪下来，组成的就是后序遍历了。

后序遍历中，根节点默认最后面

后序遍历结果：H I D J E B K F G C A

在这里插入图片描述
动画展示：
在这里插入图片描述

（4）层次遍历

层次遍历很好理解，就是从根节点开始，一层一层，从上到下，每层从左到右，依次写值就可以了

层次遍历结果：A B C D E F G H I J K

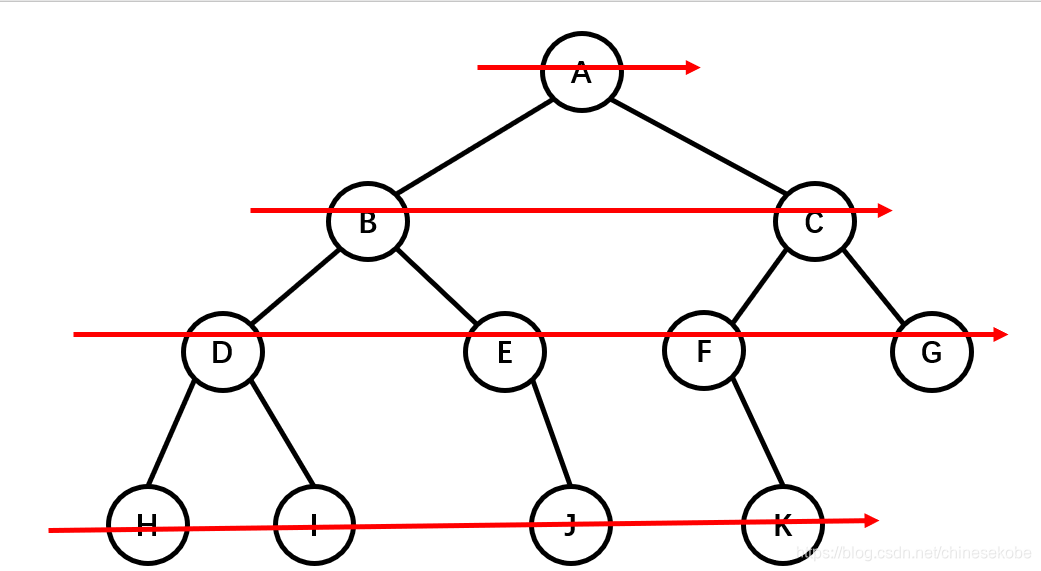
在这里插入图片描述

解释外圈跑的意思：

绕着外围跑一整圈的真正含义是：遍历所有结点时，都先往左孩子走，再往右孩子走。

（5）口诀

先序遍历： 先根 再左 再右

中序遍历： 先左 再根 再右

后序遍历： 先左 再右 再根

这里的根，指的是每个分叉子树（左右子树的根节点）根节点，并不只是最开始头顶的根节点，需要灵活思考理解，建议画图理解！！

二、代码展示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include<stdio.h>
#include<stdlib.h>

typedef struct Tree{





 int data;					//	存放数据域
 struct Tree *lchild;			//	遍历左子树指针
 struct Tree *rchild;			//	遍历右子树指针

}Tree,*BitTree;

BitTree CreateLink()
{




	int data;
	int temp;
	BitTree T;

	scanf("%d",&data);		//	输入数据
	temp=getchar();			//	吸收空格

	if(data == -1){



     			//	输入-1 代表此节点下子树不存数据，也就是不继续递归创建

		return NULL;

	}else{




		T = (BitTree)malloc(sizeof(Tree));			//		分配内存空间
		T->data = data;								//		把当前输入的数据存入当前节点指针的数据域中

		printf("请输入%d的左子树: ",data);
		T->lchild = CreateLink();					//		开始递归创建左子树
		printf("请输入%d的右子树: ",data);
		T->rchild = CreateLink();					//		开始到上一级节点的右边递归创建左右子树
		return T;							//		返回根节点
	}

}
//	先序遍历
void ShowXianXu(BitTree T)			//		先序遍历二叉树
{




	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{




		return;
	}
	printf("%d ",T->data);
	ShowXianXu(T->lchild);			//	递归遍历左子树
	ShowXianXu(T->rchild);			//	递归遍历右子树
}
//	中序遍历
void ShowZhongXu(BitTree T)			//		先序遍历二叉树
{




	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{




		return;
	}

	ShowZhongXu(T->lchild);			//	递归遍历左子树
	printf("%d ",T->data);
	ShowZhongXu(T->rchild);			//	递归遍历右子树

}
//	后序遍历
void ShowHouXu(BitTree T)			//		后序遍历二叉树
{




	if(T==NULL)						//	递归中遇到NULL，返回上一层节点
	{




		return;
	}

	ShowHouXu(T->lchild);			//	递归遍历左子树
	ShowHouXu(T->rchild);			//	递归遍历右子树
	printf("%d ",T->data);
}


int main()
{




	BitTree S;
	printf("请输入第一个节点的数据:\n");
	S = CreateLink();			//		接受创建二叉树完成的根节点
	printf("先序遍历结果: \n");
	ShowXianXu(S);				//		先序遍历二叉树

	printf("\n中序遍历结果: \n");
	ShowZhongXu(S);				//		中序遍历二叉树

	printf("\n后序遍历结果: \n");
	ShowHouXu(S);				//		后序遍历二叉树

	return 0;
}